Roger Guimerà
Físic i investigador ICREA al Departament d'Enginyeria Química de la URV.
L'estadística té un paper cada cop més important en els esports professionals, des del futbol (en què llegim estadístiques sobre gols esperats en un partit o la probabilitat de marcar des d'una certa posició) fins al beisbol (esport que va ser pioner en l'ús de l'estadística i en què fins i tot decisions com quin jugador cal fitxar es prenen amb el full de càlcul a la mà), per posar-ne un parell d'exemples.
Al món casteller, una de les qüestions més susceptibles d'encetar una discussió és la del mèrit de cadascun dels castells. Què és més difícil fer: un 2de8sf o un 4de9sf? Un 3de10fm o un 4de10fm? Aquesta pregunta pren una rellevància especial un cop cada dos anys, al Concurs de Castells de Tarragona, en què les colles competeixen (malgrat algunes reticències a fer servir la paraula) per veure qui aconsegueix més punts. Però és possible assignar uns "punts" a cada castell? Podem establir, de manera objectiva, el valor de cada construcció?
La dificultat per calcular el mèrit d'un castell rau en el fet que no podem demanar a totes les colles que, en un dia concret de l'any, provin de fer tots els castells. Si ho poguéssim fer, aleshores seria relativament fàcil d'endreçar els castells per ordre de dificultat: com menys colles siguin capaces de descarregar un castell, més meritori és. Cada colla, però, en cada diada, intenta de fer uns castells concrets, i cada colla té un nivell diferent, de manera que només tenim comparacions parcials de la dificultat de les construccions. A més, les colles no poden assajar tots els castells i cadascuna fa la seva tria en funció dels objectius de temporada. Potser l'única cosa que podem fer és constituir un grup d'experts que n'estableixin les dificultats... o potser podem fer servir les matemàtiques.
Si en una diada concreta una colla prova de fer dos castells i un li surt millor que l'altre (diguem que descarrega el primer però només carrega el segon), això seria indicatiu que un (el segon) és més difícil que l'altre. Evidentment, el resultat podria ser fruit de l'atzar però, com més diferència de dificultat hi hagi entre dues construccions, més difícil serà que hi hagi una sorpresa. Per exemple, si una colla prova un 4d7 i un 4d8 i un li surt millor que l'altre, és pràcticament segur que el que ha sortit millor és el 4d7, que és molt més senzill. Per contra, si els castells són un 2d8 i un 3d10fm, a vegades serà un el que surti millor i d'altres serà l'altre perquè són castells de dificultat semblant.
La solució matemàtica al problema de quantificar el mèrit de cada castell implica plasmar aquesta idea intuïtiva en un model matemàtic. Comencem per fer explícita la suposició que cada castell té una dificultat intrínseca, que és desconeguda i és, precisament, el que volem estimar. A continuació, tornem a la situació hipotètica en què, el mateix dia, una colla prova dos castells, A i B, i B surt millor que A; modelitzem matemàticament aquesta situació dient que la probabilitat que el castell B surti millor que l'A -en lloc de fer-ho a la inversa - , depèn només de la diferència entre les respectives dificultats, tal com es mostra a la figura següent.
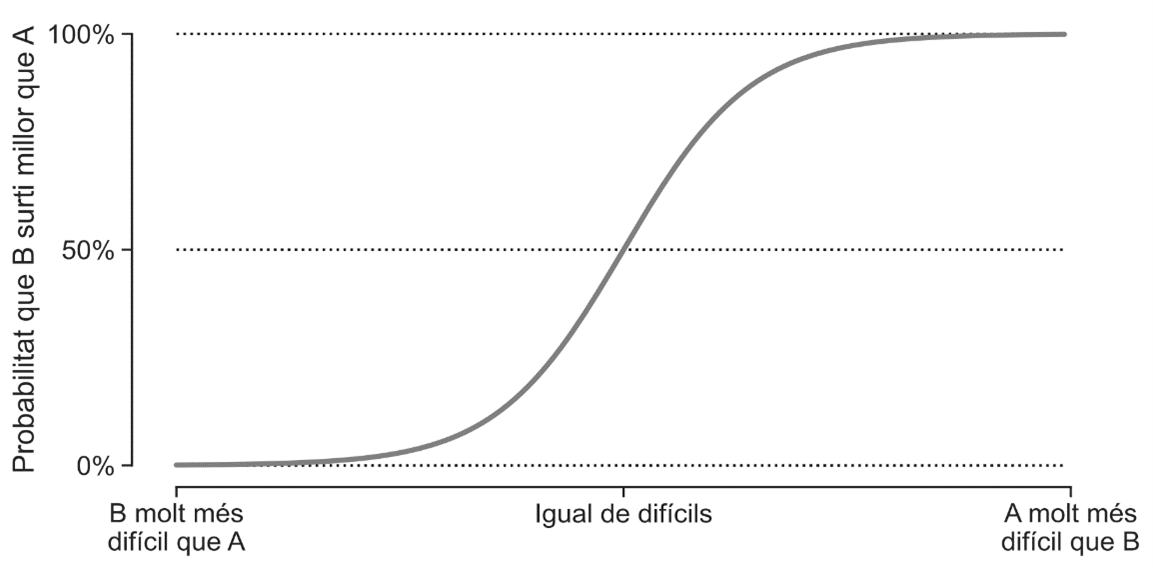
La funció que ens dona la probabilitat d'acord amb la diferència de dificultats és l'anomenada funció logística, i té un paper importantíssim en àrees diverses de la ciència i la tecnologia, des de models físics dels sistemes magnètics fins a la intel·ligència artificial.
Sigui com sigui, un cop tenim el model formulat en termes matemàtics d'aquesta manera, només cal esbrinar quina és la dificultat de cada castell mitjançant un algoritme. Al principi, l'algoritme no té ni idea de les dificultats, de manera que assigna a cada castell una dificultat a l'atzar. Com que aquesta assignació inicial és totalment aleatòria, pot passar que, per exemple, li assignem més dificultat a un 4de7 que a un 4de8. Però, si això passa, el model predirà que el 4d8 ha de sortir sovint millor que el 4d7 (quan els intenta la mateixa colla i el mateix dia), cosa que és clarament contrafactual: les dades històriques dels castells diuen exactament el contrari. Aquesta observació permet a l'algoritme reajustar les dificultats, de manera que apuja la dificultat del 4de8 i abaixa la del 4de7.
Repetint aquest procés milions de vegades, podem arribar a estimar la complexitat de cada castell: l'algoritme precís que fa arribar les dificultats als seus valors més plausibles amb les dades històriques ( cal precisar que els més plausibles no vol dir els únics possibles perquè, com passa amb tota l'anàlisi matemàtica, hi ha incertesa) el va idear el matemàtic alemany Ernst Zermelo el 1929. L'any 2022, quasi cent anys després, el físic anglès Mark Newman ha proposat una variació de l'algoritme que permet arribar a la mateixa solució però molt més ràpidament.
I doncs, quina és la dificultat intrínseca de cada castell si fem servir l'algoritme de Zermelo i dades històriques de les diades castelleres? Per respondre aquesta pregunta hem recollit dades de 75.525 castells fets entre 1990 i 2022, a partir de la base de dades de la Coordinadora de Colles Castelleres de Catalunya (no s'han comptabilitzat els intents desmuntats, ni els pilars de 4 i de 5 i tampoc els castells que no tenen puntuació al Concurs ni els que són exclusivament universitaris).
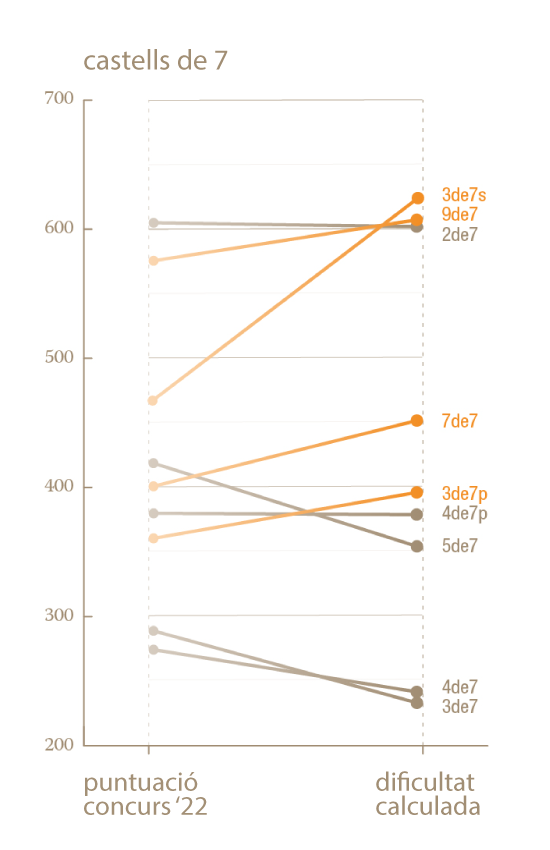
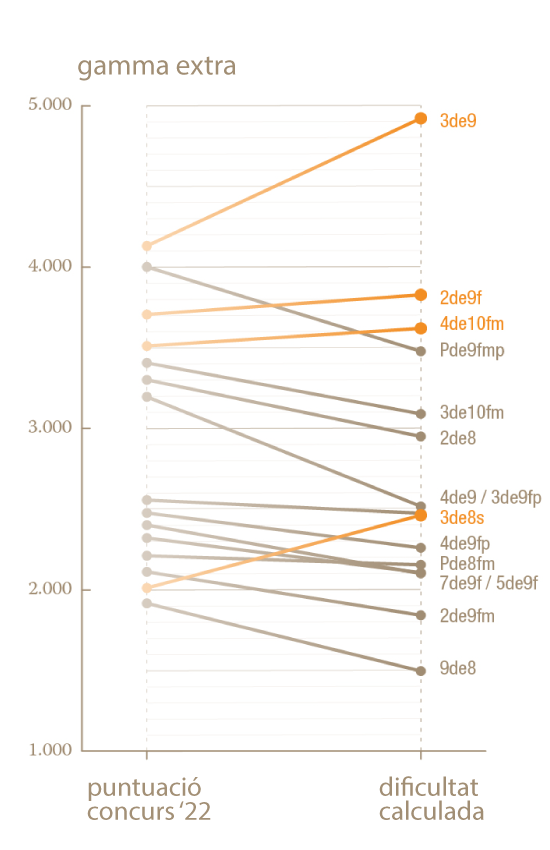
Als següents gràfics comparem les dificultats obtingudes matemàticament amb l'algoritme i les puntuacions del Concurs de Castells de l'any 2022 en funció de si són castells de gamma extra, castells de 9 o castells de 9 i de 8 i castells de 7. Els castells representats en taronja són castells que, segons el model matemàtic, mereixerien més punts dels que tenen actualment al concurs. I, a la inversa, els castells en gris són els que en mereixerien menys.
Veiem que tot plegat és força consistent. Per exemple, segons els dos criteris, el castell més meritori és el 3de9 sense folre. De fet, els vuit castells més difícils segons la puntuació i la dificultat calculada matemàticament són exactament els mateixos. L'ordenació també és semblant però no sempre idèntica: mentre que segons la puntuació del concurs, el Pde9fmp és el segon castell més difícil, segons la dificultat matemàtica ho seria el 2de9f.
I si un algoritme establís la dificultat dels castells?
