Roger Guimerà
Físico e investigador ICREA en el Departamento de Ingeniería Química de la URV
La estadística tiene un papel cada vez más importante en los deportes profesionales, desde el fútbol (en el que leemos estadísticas sobre goles esperados en un partido o la probabilidad de marcar desde cierta posición) hasta el béisbol (deporte que fue pionero en el uso de la estadística y en la que incluso decisiones como qué jugador se debe fichar se toman con la hoja de cálculo en la mano), para poner un par de ejemplos.
En el mundo casteller, una de las cuestiones más susceptibles para empezar una discusión es la del mérito de cada uno de los castells. ¿Qué es más difícil conseguir: un 2de8sf o un 4de9sf? ¿Un 3de10fm o un 4de10fm? Esta pregunta toma una relevancia especial una vez cada dos años, en el Concurso Internacional de Castells de Tarragona, en el que los grupos compiten (a pesar de algunas reticencias a utilizar la palabra) para ver quién consigue más puntos. ¿Pero es posible asignar unos "puntos" a cada castell? ¿Podemos establecer, de forma objetiva, el valor de cada construcción?
La dificultad para calcular el mérito de un castell radica en que no podemos pedir a todas las colles que, en un día concreto del año, traten de hacer todos los castells. Si pudiéramos hacerlo, entonces sería relativamente fácil clasificar los castells por orden de dificultad: cuanto menos colles sean capaces de descargar un castell, más meritorio es. Pero cada colla, en cada día, intenta hacer unos castells concretos, y cada colla tiene un nivel diferente, de manera que sólo tenemos comparaciones parciales de la dificultad de las construcciones. Además, las colles no pueden ensayar todos los castells y cada una de ellas hace su elección en función de los objetivos de temporada. Quizás lo único que podemos hacer es constituir un grupo de expertos que establezcan sus dificultades... o quizás podemos utilizar las matemáticas.
Si en un día concreto una colla intenta hacer dos castells y uno le sale mejor que el otro (digamos que descarga el primero pero sólo carga el segundo), esto sería indicativo de que uno (el segundo) es más difícil que el otro. Evidentemente, el resultado podría ser fruto del azar pero, a mayor diferencia de dificultad entre dos construcciones, más difícil será que haya una sorpresa. Por ejemplo, si una colla prueba un 4d7 y un 4d8 y uno le sale mejor que el otro, es prácticamente seguro que lo que ha salido mejor es el 4d7, que es mucho más sencillo. Por el contrario, si los castells son un 2d8 y un 3d10fm, a veces será uno el que mejor salga y otras será el otro porque son castells de dificultad parecida.
La solución matemática al problema de cuantificar el mérito de cada castell implica plasmar esa idea intuitiva en un modelo matemático. Empecemos por hacer explícita la suposición de que cada castell tiene una dificultad intrínseca, que es desconocida y es, precisamente, lo que queremos amar. A continuación, volvemos a la situación hipotética en la que, el mismo día, un grupo prueba dos castells, A y B, y B sale mejor que A; modelizamos matemáticamente esta situación diciendo que la probabilidad de que el castell B salga mejor que el A -en lugar de hacerlo a la inversa-, depende sólo de la diferencia entre las respectivas dificultades, tal y como se muestra en la siguiente figura.
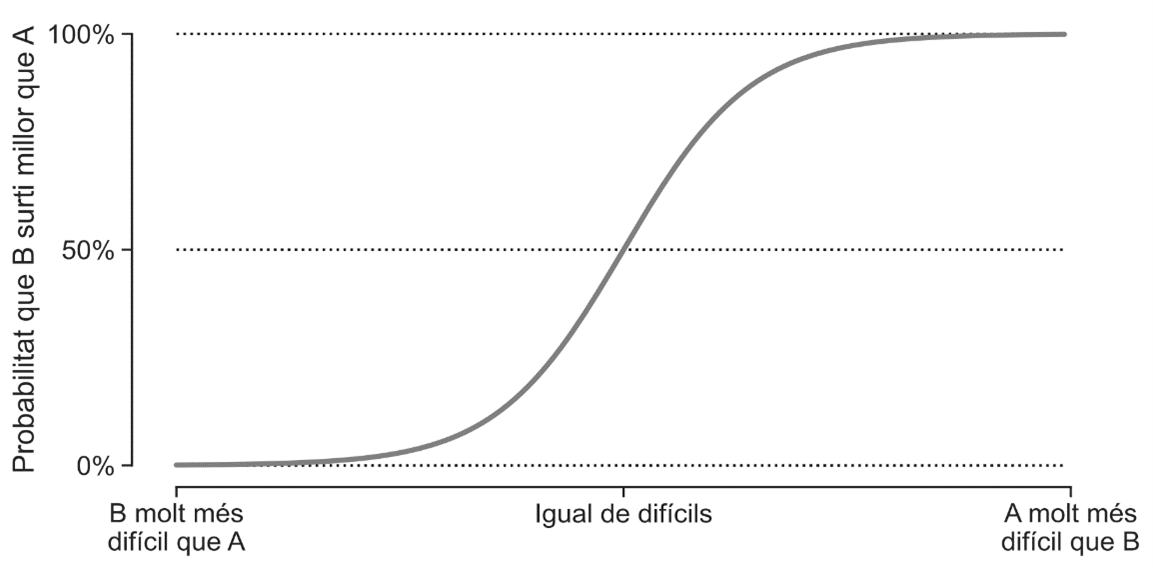
La función que nos da la probabilidad de acuerdo con la diferencia de dificultades es la llamada función logística, y desempeña un papel importantísimo en áreas diversas de la ciencia y la tecnología, desde modelos físicos de los sistemas magnéticos hasta la inteligencia artificial.
Sea como fuere, una vez tenemos el modelo formulado en términos matemáticos de esta manera, basta con averiguar cuál es la dificultad de cada castell mediante un algoritmo. Al principio, el algoritmo no tiene ni idea de las dificultades, por lo que asigna a cada castell una dificultad al azar. Dado que esta asignación inicial es totalmente aleatoria, puede ocurrir que, por ejemplo, le asignemos más dificultad a un 4de7 que a un 4de8. Pero, si esto ocurre, el modelo predecirá que el 4d8 debe salir a menudo mejor que el 4d7 (cuando los intenta ela misma colla y el mismo día), lo que es claramente contrafactual: los datos históricos de los castells dicen exactamente lo contrario. Esta observación permite al algoritmo reajustar las dificultades, subiendo la dificultad del 4de8 y bajando la del 4de7.
Repitiendo este proceso millones de veces, podemos llegar a estimar la complejidad de cada castell: el algoritmo preciso que hace llegar las dificultades a sus valores más plausibles con los datos históricos (hay que precisar que los más plausibles no significa los únicos posibles porque, como ocurre con todo el análisis matemático, hay incertidumbre) lo ideó el matemático alemán Ernst Zermelo en 1929. En 2022, casi cien años después, el físico inglés Mark Newman ha propuesto una variación del algoritmo que permite llegar en la misma solución pero mucho más rápidamente.
Así pues, ¿cuál es la dificultad intrínseca de cada castell si utilizamos el algoritmo de Zermelo y datos históricos de los festejos castellers? Para responder a esta pregunta hemos recogido datos de 75.525 castells hechos entre 1990 y 2022, a partir de la base de datos de la Coordinadora - Jove de Tarragona (no se han contabilizado los intentos desmontados, ni los pilares de 4 y de 5 y tampoco los castells que no tienen puntuación en el Concurso ni los que son exclusivamente universitarios).
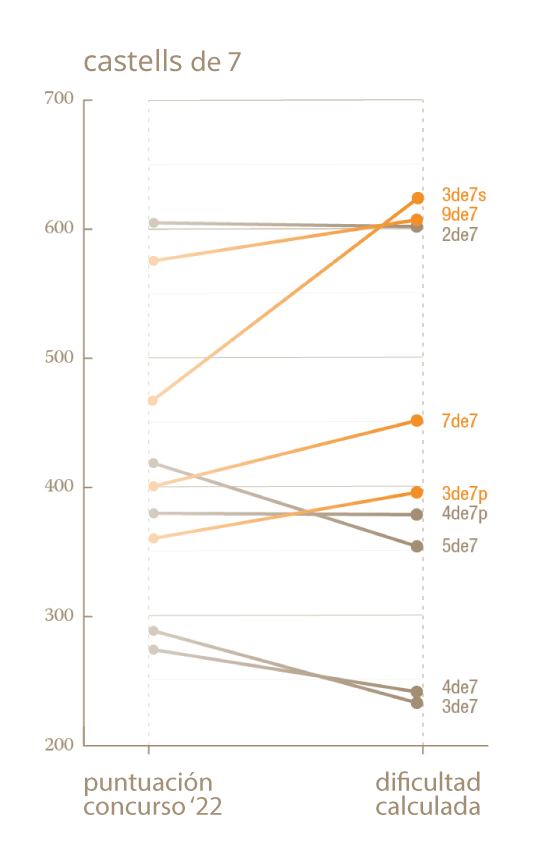
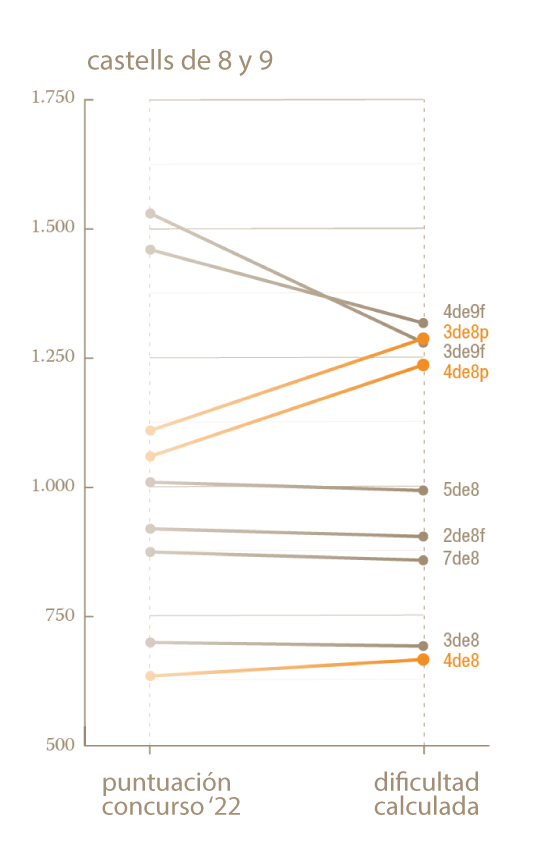
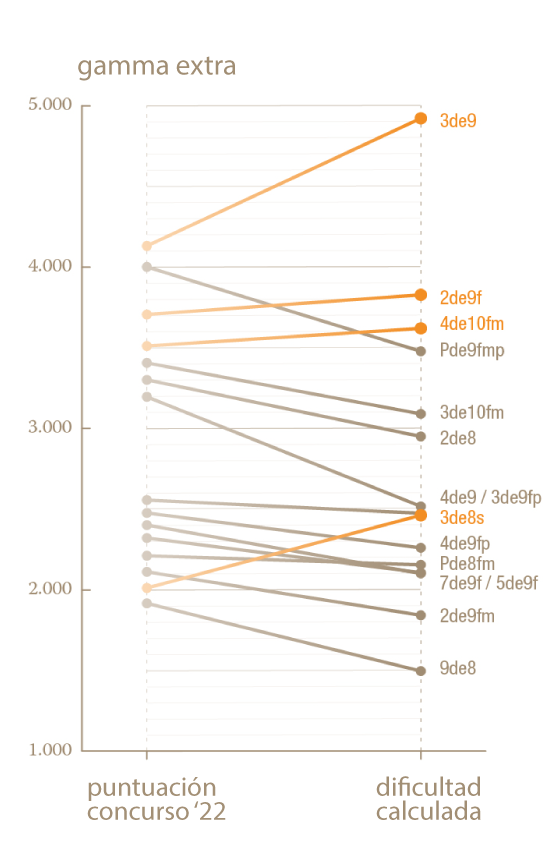
En los siguientes gráficos comparamos las dificultades obtenidas matemáticamente con el algoritmo y las puntuaciones del Concurso de Castells del año 2022 en función de si son castells de gama extra, castells de 9 y de 8 y castells de 7. Los castells representados en naranja son aquellos que, según el modelo matemático, merecerían más puntos de los que tienen actualmente en el concurso. Y, a la inversa, los castells en gris son los que menos merecerían.
Vemos que todo esto es bastante consistente. Por ejemplo, según ambos criterios, el castell más meritorio es el 3de9 sin folre. De hecho, los ocho castells más difíciles en función de la puntuación y la dificultad calculada matemáticamente son exactamente los mismos. La ordenación también es similar pero no siempre idéntica: mientras que según la puntuación del concurso, el Pde9fmp es el segundo castell más difícil, según la dificultad matemática lo sería el 2de9f.
¿Y si un algoritmo estableciese la dificultad de los castells?
