Roger Guimerà
Physicist and ICREA researcher at the Chemical Engineering Department of the URV.
In the world of human-tower building, one of the most hotly debated questions is the merit of each type of tower. Which is the hardest to build: a 2 by 8 without a cover or a 4 by 9 without a cover? A 3 by 10 with a cover and shackles or a 4 by 10 with a cover and shackles? This question takes on special relevance once every two years, at the Tarragona Human Tower Building Competition, in which teams compete (despite some reluctance to use the word) to see who gets the most points. But is it possible to assign "points" to each tower? Can we objectively establish the value of each construction?
The difficulty of calculating the merit of a particular tower lies in the fact that we cannot ask all the teams to try to build all the towers on one specific day of the year. If we could, then it would be relatively easy to arrange the towers in order of difficulty: the fewer teams able to complete a tower, the more merit it has. However, whenever they perform, teams make a selection of towers to build, and each team has a different level, so any comparisons we make of the difficulty of the constructions are not wholly reliable. Also, the teams do not practise all the towers possible; they make a choice based on their objectives for the season. Maybe the only thing we can do is to set up a group of experts to determine the difficulty of each one... or maybe we can use mathematics.
If on one specific day a team tries to build two towers and does one better than the other (let's say it completes the first but only crowns the second), this would suggest that one (the second) is more difficult than the other. Obviously, the result could be chance, but the greater the difference in difficulty between two constructions, the harder it will be for chance to play a role. For example, if a group tries a 4 by 7 and a 4 by 8 and does one better than the other, it is almost certain that this will be the 4 by 7, which is much simpler. On the other hand, if the towers are a 2 by 8 and a 3 by 10 with a cover and shackles, sometimes the first will be done better than the second and sometimes the second better than the first because they are of similar difficulty.
The mathematical solution to the problem of quantifying the merit of each tower involves translating this intuitive idea into a mathematical model. We begin by making the explicit assumption that each tower has an intrinsic difficulty, which is unknown and needs to be estimated. Then, we go back to the hypothetical situation in which, on the same day, a team tries to build two towers, A and B, and B turns out better than A. We mathematically model this situation by saying that the probability of tower B turning out better than A - instead of the other way around - depends only on the difference between the respective difficulties, as shown in the figure below.
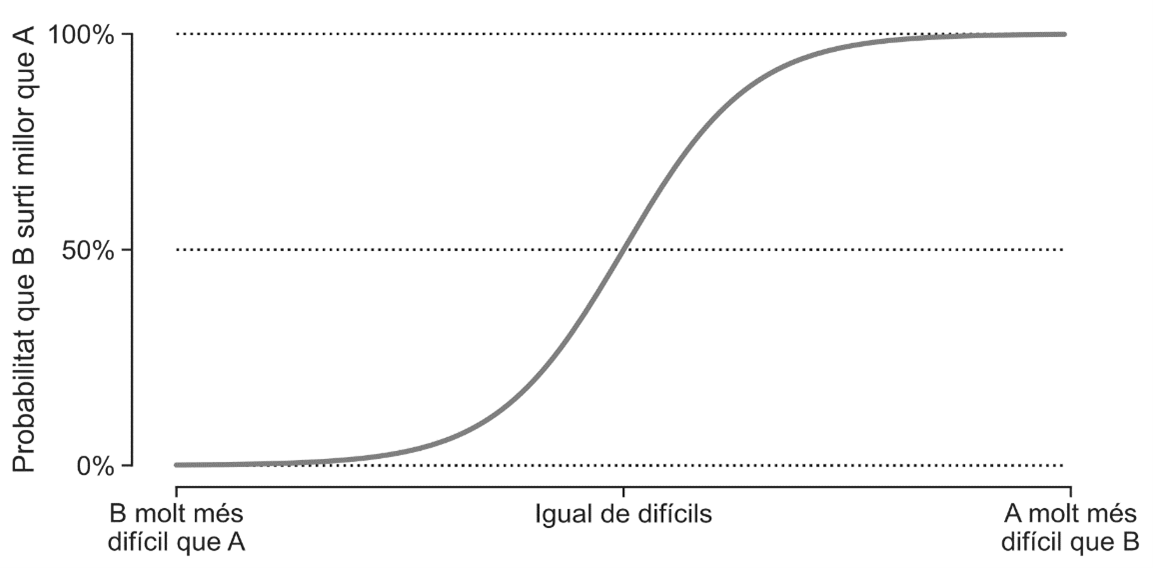
The function that gives us the probability on the basis of the difference in difficulty is the so-called logistic function. It plays a very important role in various areas of science and technology, from physical models of magnetic systems to artificial intelligence.
Whatever the case may be, once we have formulated the model in mathematical terms, we just need to determine what the difficulty of each tower is by using an algorithm. At first, the algorithm has no idea about the difficulties, so it assigns each tower a difficulty randomly. Since this initial assignment is completely random, it may, for example, assign a greater difficulty to a 4 by 7 than to a 4 by 8. But if it does, the model will predict that a 4 by 8 will often turn out better than a 4 by 7 (when done by the same team on the same day), which is clearly counterfactual. The historical data on human tower building says exactly the opposite. This observation allows the algorithm to readjust the difficulties, so it increases the difficulty of a 4 by 8 and decreases that of a 4 by 7.
By repeating this process millions of times, we can estimate the complexity of each tower: the exact algorithm that generates the most plausible difficulties using historical data (it should be pointed out that the most plausible does not mean the only ones possible because, as with all mathematical analysis, there is uncertainty) was devised by the German mathematician Ernst Zermelo in 1929. In the year 2022, almost a hundred years later, the English physicist Mark Newman proposed a variation of the algorithm that reaches the same solution but much faster.
So, what is the intrinsic difficulty of each human tower if we use Zermelo's algorithm and historical data from human-tower exhibitions? To answer this question, we collected data from 75,525 towers built between 1990 and 2022 from the database of the Coordinating Committee of Human Tower Teams of Catalonia. Any attempts that were dismantled were not counted, and neither were the pillars of 4 and 5, the towers that do not have a score assigned in the Competition or the towers that are built exclusively by university teams.
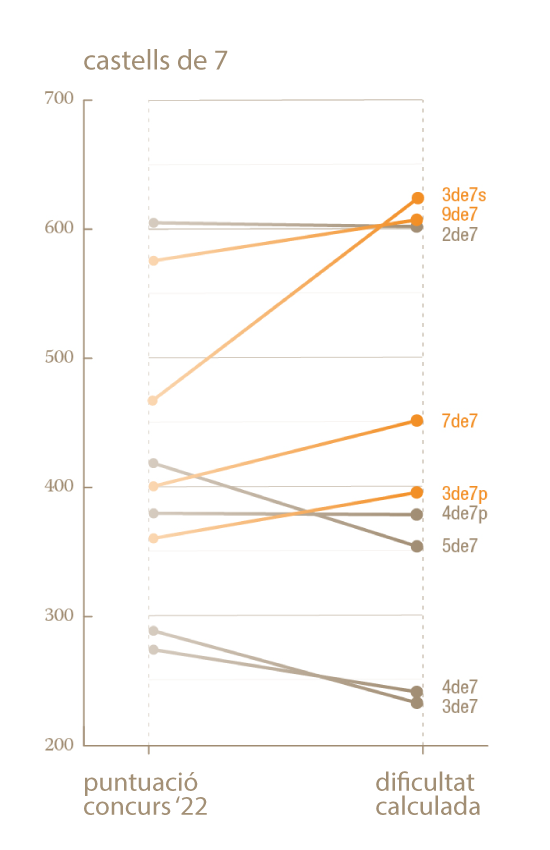
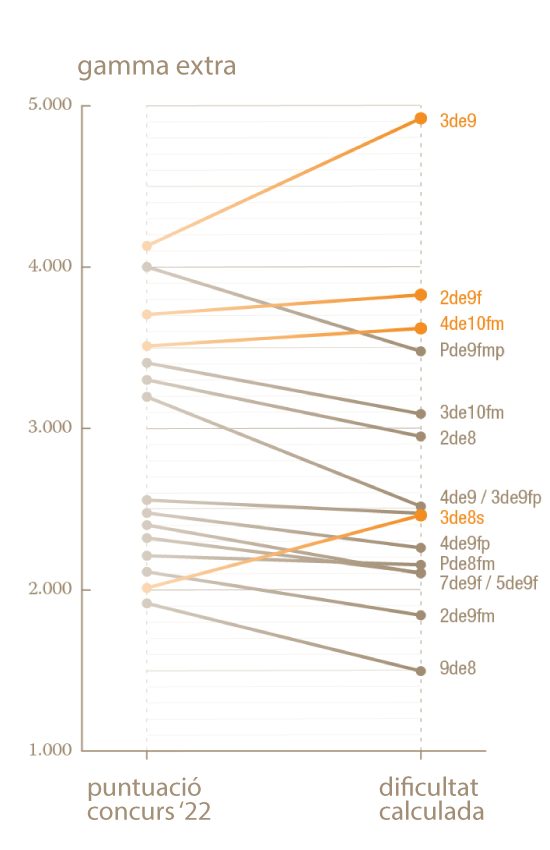
In the next figures we compare the difficulties obtained mathematically with the algorithm and the scores of the Tower-Building Competition in 2022 depending on if they are extra range human towers, 9 and 8 castels or 7 castels. The towers represented in orange are the ones that should be awarded more points than they currently are in the contest. On the other hand, the towers in grey are the ones that should be awarded fewer.
Overall, everything is quite consistent. For example, according to both criteria, the tower that deserves the highest score is the 3 by 9 without a cover. In fact, the eight most difficult towers according to the scale of points awarded and the mathematical calculation are exactly the same. The order is also similar but not identical: while according to the points awarded by the competition, the pillar of nine with a cover, shackles and prop is the second most difficult tower, according to the mathematical difficulty it is the 2 by 9 with a cover. So what do you think? Should the difficulty of human towers be determined by an algorithm?
